Analisi matematica vol. 3 - Funzioni di più variabili Parte I e II

Šilov Gheorghij Evghenievic

Analisi matematica vol. 3 - Funzioni di più variabili Parte I e II

€36.10 €38.00
Risparmia €1.90
SKU: 9788864732312
Quantità:

Contatti

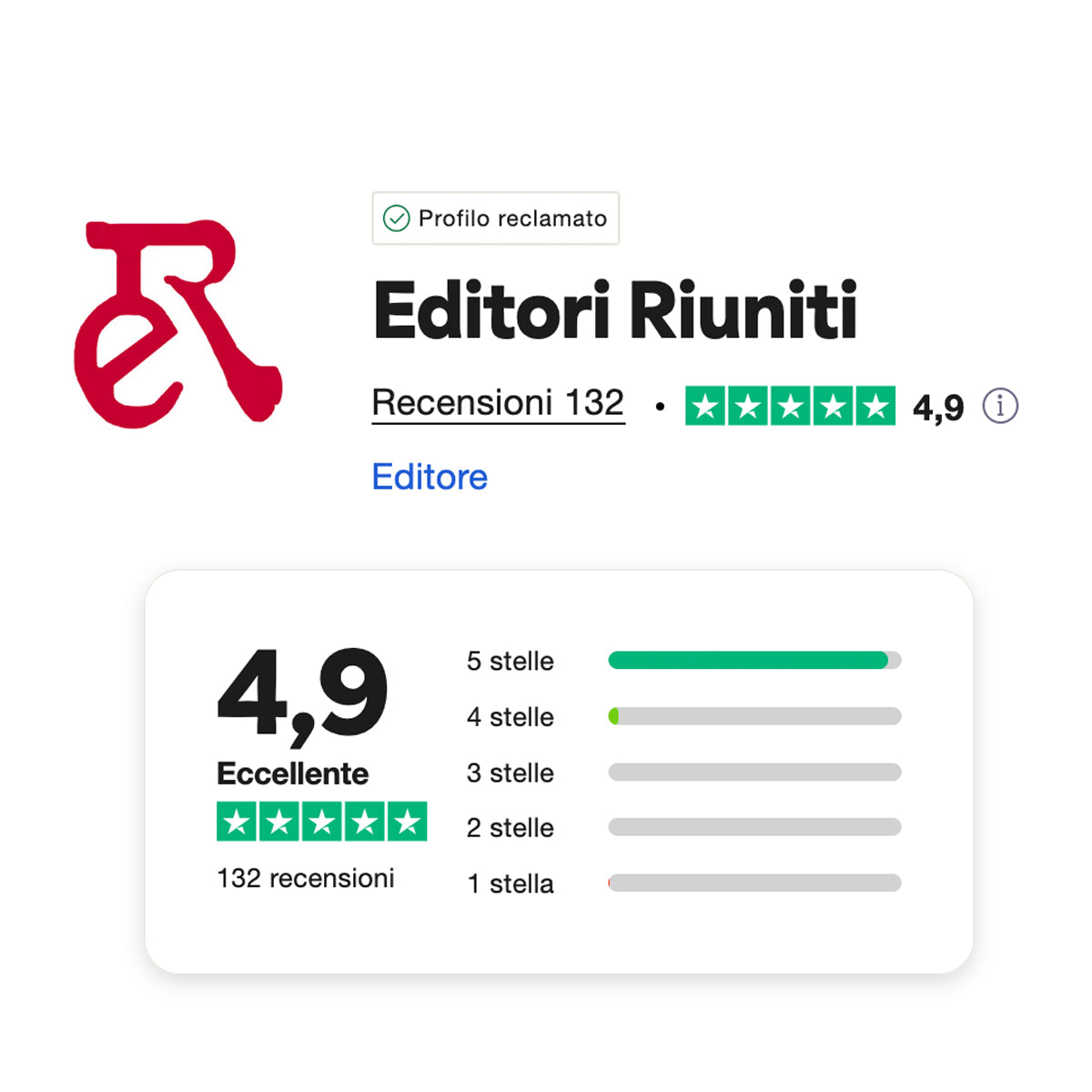
Newsletter

Per iscriverti alla newsletter trovi il form in fondo a questa pagina.

 

Email della casa editrice

info@editoririuniti.it

 

Invio manoscritti

redazione@editoririuniti.it

È gentilmente richiesto l'invio:

  • del testo (anche parziale e non definitivo) nel formato .doc oppure .pdf;
  • di una sinossi o breve presentazione dell'opera;
  • di un CV o breve biografia dell'autore/i.

    Leggiamo e valutiamo tutte le proposte, ma a causa dell'elevato numero di richieste purtroppo non ci è possibile rispondere a tutti.

    Non pubblichiamo romanzi e poesie.

     

    Invio curriculum *al momento non ci sono posizioni aperte*

    risorseumane@editoririuniti.it

    Candidature inviate ad altri indirizzi non verranno prese in considerazione.

     

    Telefono

    Casa editrice: (+39) 380 4590487

    (per informazioni su ordini e disponibilità titoli scrivere a info@editoririuniti.it)

     

    Social

    https://www.facebook.com/EditoriRiuniti

    https://www.instagram.com/editoririuniti_libri

     

    Cataloghi

    Cliccare per visualizzare e scaricare il catalogo generale e il catalogo dedicato a Matematica e Fisica.

     

    Indirizzo amministrazione

    Editori Riuniti
    Via di Fioranello, 56
    00134 Roma (RM)

     

    Promozione e distribuzione

    Siamo distribuiti su tutto il territorio nazionale da Messaggerie Libri. La promozione è affidata a EmmePromozione.

    Questo terzo volume (qui trovi il volume 1 e qui il volume 2), è costituito di due parti: Calcolo differenziale e integrale e Dagli spazi lineari alle varietà. Adottando un metodo induttivo si permette al lettore di seguire la formazione di concetti sempre più astratti e di vedere la necessità delle generalizzazioni corrispondenti.

    TRUSTPILOT